Pulay stress: Difference between revisions
No edit summary |
No edit summary |
||
| Line 11: | Line 11: | ||
Note that the structure is relaxed by minimizing the stress tensor, i.e. when the pressure is zero. If compared to the volume, the pressure minimum does not correspond to the energetic minimum, cf. Fig. 3. This is the effect of the Pulay stress. | Note that the structure is relaxed by minimizing the stress tensor, i.e. when the pressure is zero. If compared to the volume, the pressure minimum does not correspond to the energetic minimum, cf. Fig. 3. This is the effect of the Pulay stress. | ||
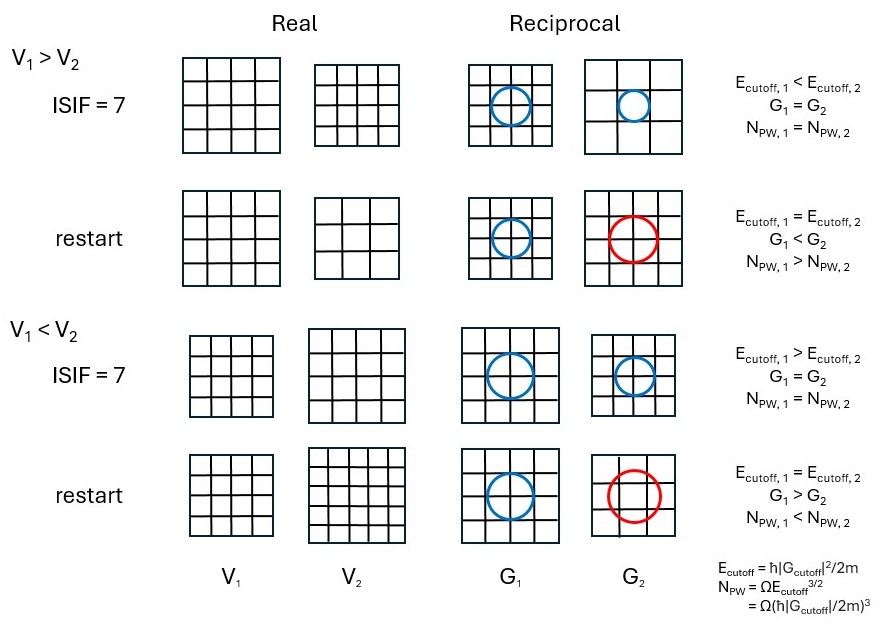
[[File:Pulay_Stress_Grids.jpg | [[File:Pulay_Stress_Grids.jpg|Fig 2. Grids.]] | ||
<!--[[Category:Ionic minimization]][[Category:Howto]]--> | <!--[[Category:Ionic minimization]][[Category:Howto]]--> | ||
==References== | ==References== | ||
Revision as of 07:23, 26 July 2024
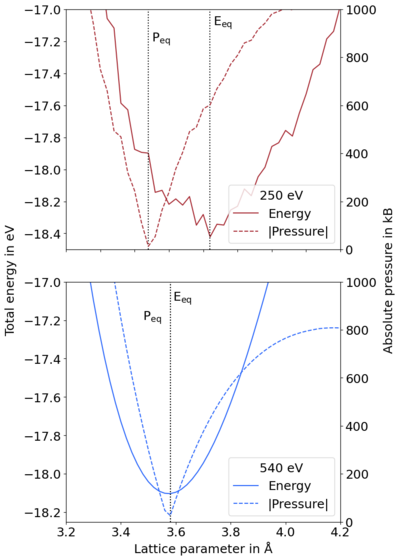
Pulay stress is unphysical stress coming from unconverged calculations with respect to basis set. It distorts the cell structure, decreasing it from the equilibrium volume and resulting in jagged energy vs. volume curves, cf. Figure 1 (top). In this article, the computational origin of this is briefly discussed, and then solutions for correcting the Pulay stress. It is important to note that problems due to the Pulay stress can often be neglected if only volume-conserving relaxations are performed. This is because the Pulay stress is, usually, nearly uniform and only changes the diagonal elements of the stress tensor by a constant amount.
Introduction
The energy for a periodic system, e.g. band structures, is calculated using a finite number of plane waves and a finite number of k-points. A fixed number of plane waves or plane wave energy cutoff may be used to set a constant basis.[1] In VASP, a constant energy cutoff is used, cf. ENCUT. The number of plane waves is related to the energy cutoff and the size of the cell :
is constant in a relaxation calculation, which means that must change to compensate for changes in . All the initial G-vectors within a sphere are included in the basis. However, when comparing cells of different sizes, i.e. during a relaxation, the cell shape is relaxed, so the direct and reciprocal lattice vectors change. The number of reciprocal G-vectors in the basis is kept fixed but the length of the G-vectors changes, indirectly changing the energy cutoff. In other words, the shape of the cutoff region changes from a sphere to an ellipsoid. This can be solved by using an infinite number of k-points and plane waves. In practice, a large enough plane wave energy cutoff and number of k-points leads to converged energies.[2] All energy changes are strictly consistent with the stress tensor; however, when the basis set is too small, i.e. prematurely truncated, this results in discontinuities in the total energy between cells of varying volumes. These discontinuities between energy and volume create stress that decreases the equilibrium volume, due to the diagonal components of the stress tensor being incorrect. This is called the Pulay stress. Figure 1 (top) show these discontinuities for diamond for prematurely truncated energy cutoffs and k-point meshes, respectively, in comparison to converged curves.
Note that the structure is relaxed by minimizing the stress tensor, i.e. when the pressure is zero. If compared to the volume, the pressure minimum does not correspond to the energetic minimum, cf. Fig. 3. This is the effect of the Pulay stress.
References
- ↑ P. Gomes Dacosta, O. Nielsen, and K. Kunc, Stress theorem in the determination of static equilibrium by the density functional method, J. Phys. C: Solid State Phys. 19, 3163 (1986).
- ↑ G. P. Francis and M. C. Payne, Finite basis set corrections to total energy pseudopotential calculations, J. Condens. Matter Phys. 2, 4395 (1990).