SAXIS: Difference between revisions
No edit summary |
No edit summary |
||
| (16 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{TAGDEF|SAXIS|[real array]| 0 | {{TAGDEF|SAXIS|[real array]| (0, 0, 1)}} | ||
Description: | Description: Set the global spin-quantization axis w.r.t. Cartesian coordinates. | ||
---- | ---- | ||
{{TAG|SAXIS}} specifies the relative orientation of spinor space spanned by the Pauli matrices <math>\{\sigma_1</math>, <math>\sigma_2</math>, <math>\mathbf{\sigma}_3\}</math> with respect to Cartesian coordinates <math>\{\hat x, \hat y, \hat z\} </math>. The default is <math>\sigma_1=\hat x</math>, <math>\sigma_2 =\hat y</math>, <math>\sigma_3 = \hat z</math>. | |||
The direction of the spin-quantization axis <math>\sigma_3</math> with respect to Cartesian coordinates is set | |||
{{TAG|SAXIS}} = s<sub>x</sub> s<sub>y</sub> s<sub>z</sub> ! global spin | {{TAG|SAXIS}} = s<sub>x</sub> s<sub>y</sub> s<sub>z</sub> ! global spin-quantization axis | ||
such that <math>\sigma_3=\mathbf{s}/|\mathbf{s}|</math>, i.e., <math>\sigma_3</math> points along <math>\mathbf{s}=(s_x,s_y,s_z)^T</math>. The directions of <math>\sigma_1</math> and <math>\sigma_2</math> are a consequence of rotating <math>\sigma_3</math> to point along <math>\mathbf{s}</math> as described below. | |||
The relative orientation of spinor space with respect to real space becomes important in case spin-orbit coupling is included ({{TAG|LSORBIT}}=True). All magnetic moments and spinor-like quantities written or read by VASP are given in the basis of the spinor space <math>\{\sigma_1</math>, <math>\sigma_2</math>, <math>\mathbf{\sigma}_3\}</math>. This includes the {{TAG|MAGMOM}} tag in the {{FILE|INCAR}} file, the total and local magnetizations in the {{FILE|OUTCAR}} and {{FILE|PROCAR}} file, the spinor-like orbitals in the {{TAG|WAVECAR}} file, and the magnetization density in the {{FILE|CHGCAR}} file. | |||
== Coordinate system == | |||
[[File:Saxis-angles.png|300px|thumb|Fig 1. Euler angles <math>\alpha</math> and <math>\beta</math> defined by <math>\mathbf{s}=(s_x,s_y,s_z)^T</math>.]] | |||
The default orientation is <math>\sigma_1=\hat x</math>, <math>\sigma_2 =\hat y</math>, <math>\sigma_3 = \hat z</math>. | |||
To set <math>\hat{\sigma}_3=s/|s|</math>, VASP applies two rotations with Euler angles | |||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
\alpha &= | \alpha&=\arctan2\left(\frac{s_y}{s_x}\right) \in [-\pi,\pi]\\ | ||
\beta &= | \beta&=\arctan2\left(\frac{\sqrt{s_x^2+s_y^2}}{s_z}\right) \in [0,\pi]. | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
Here, <math>\alpha</math> is the angle between the projection of {{TAG|SAXIS}} onto the ''xy'' plane (s<sub>x</sub>,s<sub>y</sub>,0) and the Cartesian vector <math>\hat x</math>, and <math>\beta</math> is the angle between the vector {{TAG|SAXIS}} and the Cartesian vector <math>\hat z</math>, see Fig. 1. Search for `Euler angles` in the {{FILE|OUTCAR}} file to see what VASP uses. For the default <math>\mathbf{s}=(0,0,1)</math>, <math>\alpha=0</math> and <math>\beta=0</math>. | |||
The inverse transformation | The transformation of a vector <math>\mathbf{m}=(m_1,m_2,m_3)^T</math> given in the basis <math>\{\sigma_1</math>, <math>\sigma_2</math>, <math>\mathbf{\sigma}_3\}</math> into <math>\mathbf{m}'=(m_x,m_y,m_z)^T</math> in Cartesian coordinates and its inverse transformation read | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
m | \mathbf{m}&= m_1 \sigma_1 + m_2 \sigma_2 + m_3 \sigma_3 \\ | ||
m | \mathbf{m}'&= m_x \hat x + m_y \hat y + m_z \hat z \\ | ||
m | \mathbf{m}'&= R_z^\alpha R_y^\beta \mathbf{m} \\ | ||
\mathbf{m} &= R_y^{-\beta} R_z^{-\alpha} \mathbf{m}' \\ | |||
\end{align} | \end{align} | ||
</math> | </math> | ||
where the rotation matrices are | |||
:<math> | |||
R_z^\alpha = \left(\begin{matrix} | |||
\cos(\alpha) & -\sin(\alpha) & 0 \\ | |||
\sin(\alpha) & \cos(\alpha) & 0 \\ | |||
0 & 0 & 1 \\ | |||
\end{matrix}\right), \quad | |||
R_y^\beta = \left(\begin{matrix} | |||
\cos(\beta) & 0 & \sin(\beta) \\ | |||
0 & 1 & 0 \\ | |||
-\sin(\beta) & 0 & \cos(\beta) \\ | |||
\end{matrix}\right). | |||
</math> | |||
{{NB|mind|Apply the proper basis transformation when comparing vector-like quantities and spinor-like quantities.|}} | |||
For instance, when {{TAG|LORBMOM}}=True the orbital angular momentum is written to the {{FILE|OUTCAR}} file in Cartesian coordinates. Thus, when comparing the orbital angular momentum (vector-like quantity) and the magnetization (spinor-like quantity), one has to perform a basis transformation on one of the quantities unless the bases agree (default). | |||
== Example == | |||
* In case the bases have the same orientation, i.e., <math>\sigma_1=\hat x</math>, <math>\sigma_2 =\hat y</math>, <math>\sigma_3 = \hat z</math> (default) | |||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
m_x & = & | m_x & = & m_1, \\ | ||
m_y & = & | m_y & = & m_2, \\ | ||
m_z & = & | m_z & = & m_3. | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
:For a single site this implies setting | |||
{{TAG|MAGMOM}} = m<sub>x</sub> m<sub>y</sub> m<sub>z</sub> ! magnetic moment in Cartesian coordinates | |||
{{TAG|SAXIS}} = 0 0 1 ! default | |||
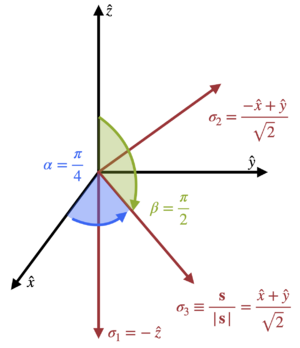
[[File:Spinor-space-example-saxis.png|300px|thumb|Fig 2. Example with <math>\mathbf{s}=(1,1,0)^T</math> and Euler angles <math>\alpha=\pi/4</math> and <math>\beta=\pi/2</math>.]] | |||
* Another good choice is setting <math>\mathbf{s}</math> to point along the direction of the on-site magnetic moment such that | |||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
m_x & = & \sin(\beta) | m_x & = & \sin(\beta)\cos(\alpha) m &= m\, s_x / \sqrt{s_x^2+s_y^2+s_z^2} \\ | ||
m_y & = & \sin(\beta) | m_y & = & \sin(\beta)\sin(\alpha) m &= m\, s_y / \sqrt{s_x^2+s_y^2+s_z^2} \\ | ||
m_z & = & \cos(\beta) m = m s_z / \sqrt{s_x^2+s_y^2+s_z^2} | m_z & = & \cos(\beta) m &= m\, s_z / \sqrt{s_x^2+s_y^2+s_z^2}, | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
:where <math>m</math> is the total on-site magnetic moment. | |||
:For a single site, this case implies setting | |||
{{TAG|MAGMOM}} = 0 0 m ! magnetic moment along sigma3 | |||
{{TAG|SAXIS}} = s<sub>x</sub> s<sub>y</sub> s<sub>z</sub> ! direction of sigma3 | |||
:Thus, there are two methods to rotate the initial magnetization in an arbitrary direction: either by changing the initial magnetic moments {{TAG|MAGMOM}} or by changing {{TAG|SAXIS}}. Both methods should, in principle, yield exactly the same energy, but for implementation reasons, the second method might be more precise. | |||
* In case | |||
{{TAG|SAXIS}} = 1 1 0 ! alpha=pi/4, beta=pi/2 | |||
:the spinor space <math>\{\sigma_1</math>, <math>\sigma_2</math>, <math>\mathbf{\sigma}_3\}</math> will be rotated with respect to real space <math>\{\hat x, \hat y, \hat z\} </math> as shown in Fig. 2. | |||
<!--- | |||
The second method also allows to read a preexisting {{FILE|WAVECAR}} file (from a collinear or non collinear run), and to continue the calculation with a different spin orientation. When a non collinear {{FILE|WAVECAR}} file is read, the spin is assumed to be parallel to {{TAG|SAXIS}} (hence VASP will initially report a magnetic moment in the ''z''-direction only). | |||
The recommended procedure for the calculation of magnetic anisotropies is therefore (please check the section on {{TAG|LMAXMIX}}): | The recommended procedure for the calculation of magnetic anisotropies is therefore (please check the section on {{TAG|LMAXMIX}}): | ||
| Line 86: | Line 105: | ||
VASP reads in the {{FILE|WAVECAR}} and {{FILE|CHGCAR}} files, aligns the spin quantization axis parallel to {{TAG|SAXIS}}, which implies that the magnetic field is now parallel to {{TAG|SAXIS}}, and performs a non selfconsistent calculation. By comparing the energies for different orientations the magnetic anisotropy can be determined. Please mind, that a completely selfconsistent calculation ({{TAG|ICHARG}} = 1) is in principle also possible with VASP, but this would allow the spinor wavefunctions to rotate from their initial orientation parallel to {{TAG|SAXIS}} until the correct groundstate is obtained, i.e. until the magnetic moment is parallel to the easy axis. In practice this rotation will be slow, however, since reorientation of the spin gains little energy. Therefore if the convergence criterion is not too tight, sensible results might be obtained even for fully selfconsistent calculations (in the few cases we have tried this worked beautifully). | VASP reads in the {{FILE|WAVECAR}} and {{FILE|CHGCAR}} files, aligns the spin quantization axis parallel to {{TAG|SAXIS}}, which implies that the magnetic field is now parallel to {{TAG|SAXIS}}, and performs a non selfconsistent calculation. By comparing the energies for different orientations the magnetic anisotropy can be determined. Please mind, that a completely selfconsistent calculation ({{TAG|ICHARG}} = 1) is in principle also possible with VASP, but this would allow the spinor wavefunctions to rotate from their initial orientation parallel to {{TAG|SAXIS}} until the correct groundstate is obtained, i.e. until the magnetic moment is parallel to the easy axis. In practice this rotation will be slow, however, since reorientation of the spin gains little energy. Therefore if the convergence criterion is not too tight, sensible results might be obtained even for fully selfconsistent calculations (in the few cases we have tried this worked beautifully). | ||
---> | |||
== Related | == Related tags and articles == | ||
{{TAG|LNONCOLLINEAR}}, | {{TAG|LNONCOLLINEAR}}, | ||
{{TAG|MAGMOM}}, | {{TAG|MAGMOM}}, | ||
{{TAG|LSORBIT}} | {{TAG|LSORBIT}} | ||
{{sc|SAXIS|Examples|Examples that use this tag}} | |||
---- | ---- | ||
[[Category:INCAR]] | [[Category:INCAR tag]][[Category:Magnetism]][[Category:Noncollinear magnetism]] | ||
Latest revision as of 09:55, 21 September 2023
SAXIS = [real array]
Default: SAXIS = (0, 0, 1)
Description: Set the global spin-quantization axis w.r.t. Cartesian coordinates.
SAXIS specifies the relative orientation of spinor space spanned by the Pauli matrices , , with respect to Cartesian coordinates . The default is , , . The direction of the spin-quantization axis with respect to Cartesian coordinates is set
SAXIS = sx sy sz ! global spin-quantization axis
such that , i.e., points along . The directions of and are a consequence of rotating to point along as described below.
The relative orientation of spinor space with respect to real space becomes important in case spin-orbit coupling is included (LSORBIT=True). All magnetic moments and spinor-like quantities written or read by VASP are given in the basis of the spinor space , , . This includes the MAGMOM tag in the INCAR file, the total and local magnetizations in the OUTCAR and PROCAR file, the spinor-like orbitals in the WAVECAR file, and the magnetization density in the CHGCAR file.
Coordinate system
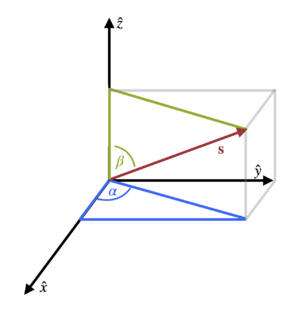
The default orientation is , , . To set , VASP applies two rotations with Euler angles
Here, is the angle between the projection of SAXIS onto the xy plane (sx,sy,0) and the Cartesian vector , and is the angle between the vector SAXIS and the Cartesian vector , see Fig. 1. Search for `Euler angles` in the OUTCAR file to see what VASP uses. For the default , and .
The transformation of a vector given in the basis , , into in Cartesian coordinates and its inverse transformation read
where the rotation matrices are
| Mind: Apply the proper basis transformation when comparing vector-like quantities and spinor-like quantities. |
For instance, when LORBMOM=True the orbital angular momentum is written to the OUTCAR file in Cartesian coordinates. Thus, when comparing the orbital angular momentum (vector-like quantity) and the magnetization (spinor-like quantity), one has to perform a basis transformation on one of the quantities unless the bases agree (default).
Example
- In case the bases have the same orientation, i.e., , , (default)
- For a single site this implies setting
MAGMOM = mx my mz ! magnetic moment in Cartesian coordinates SAXIS = 0 0 1 ! default
- Another good choice is setting to point along the direction of the on-site magnetic moment such that
- where is the total on-site magnetic moment.
- For a single site, this case implies setting
MAGMOM = 0 0 m ! magnetic moment along sigma3 SAXIS = sx sy sz ! direction of sigma3
- Thus, there are two methods to rotate the initial magnetization in an arbitrary direction: either by changing the initial magnetic moments MAGMOM or by changing SAXIS. Both methods should, in principle, yield exactly the same energy, but for implementation reasons, the second method might be more precise.
- In case
SAXIS = 1 1 0 ! alpha=pi/4, beta=pi/2
- the spinor space , , will be rotated with respect to real space as shown in Fig. 2.
Related tags and articles
LNONCOLLINEAR, MAGMOM, LSORBIT
